Bootstrap Boosting

Wrapper function for applying bootstrap estimation using gradient boosting.

## Bootstrap boosting.
bboost(..., data, type = 1, cores = 1,
  n = 2, prob = 0.623, fmstop = NULL,
  trace = TRUE, drop = FALSE, replace = FALSE)

## Plotting function.
bboost_plot(object, col = NULL)

## Predict method.
# S3 method for bboost
predict(object, newdata, ..., cores = 1, pfun = NULL)

Arguments

...

Arguments passed to bamlss and predict.bamlss.

data

The data frame to be used for modeling.

type

Type of algorithm, type = 1 uses all observations and samples with replacement, type = 2 uses only a fraction specified in prob and samples with replacement.

cores

The number of cores to be used.

n

The number of bootstrap iterations.

prob

The fraction that should be used to fit the model in each bootstrap iteration.

fmstop

The function that should return the optimum stopping iteration. The function must have two arguments: (1) the model end (2) the data. The function must return a list with two named arguments: (1) "mstop" the optimum stopping iteration and (2) a vector of the objective criterion that should be evaluated by the hold out sample data during each bootstrap iteration. See the examples.

trace

Prints out the current state of the bootstrap algorithm.

drop

Should only the best set of parameters be saved?

replace

Sampling with replacement, or sampling ceiling(nobs * prob) rows of the data for fitting the n models.

object

The "bboost" object used for prediction and plotting.

col

The color that should be used for plotting.

newdata

The data frame predictions should be made for.

pfun

The prediction function that should be used, for example predictn could be used, too. Note that this is experimental.

Value

A list of bamlss objects.

See also

bamlss, boost, lasso, BayesX

Examples

if (FALSE) ## Simulate data.
set.seed(123)
d <- GAMart()

## Estimate model.
f <- num ~ s(x1) + s(x2) + s(x3) + s(lon,lat)

## Function for evaluation of hold out sample
## criterion to find the optimum mstop.
fmstop <- function(model, data) {
  p <- predict(model, newdata = data, model = "mu")
  mse <- NULL
  for(i in 1:nrow(model$parameters))
    mse <- c(mse, mean((data$num - p[, i])^2))
  list("MSE" = mse, "mstop" = which.min(mse))
}

## Bootstrap boosted models.
b <- bboost(f, data = d, n = 50, cores = 3, fmstop = fmstop)

## Plot hold out sample MSE.
bboost_plot(b)


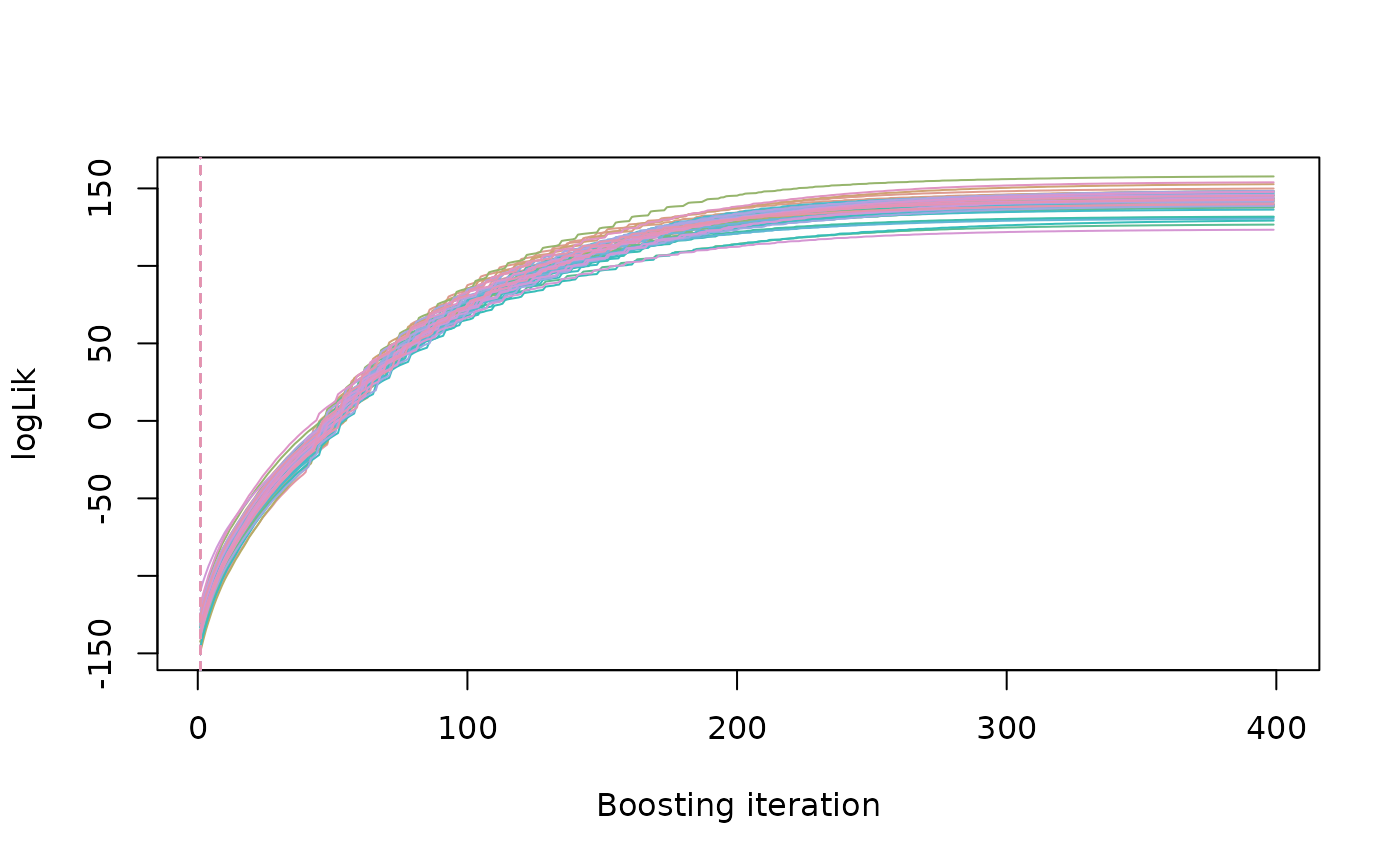## Predict for each bootstrap sample.
nd <- data.frame("x2" = seq(0, 1, length = 100))
p <- predict(b, newdata = nd, model = "mu", term = "x2")
plot2d(p ~ x2, data = nd)
#> Error in h(simpleError(msg, call)): error in evaluating the argument 'x' in selecting a method for function 'as.matrix': object 'p' not found